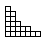
Figure 1. Un exemple de profil de dune abstrait : une suite de colonnes de grains, de hauteurs décroissantes de gauche à droite. Comme la forme des grains n'a pas d'importance dans ce qui nous intéresse ici, nous les représentons par des carrés.
Le problème.
Voilà un article qui commence bien, puisqu'il vous demande d'aller sur la plage. Mais, pour une fois, tournez le dos à la mer et observez les belles dunes vallonnées qui elles aussi sont signes de vacances réussies. Ces dunes sont constituées de milliards de minuscules grains de sable. Ils sont tous différents, par leur forme, leur masse, leur taille, etc. Toutefois, on peut en un premier temps ignorer ces différences et supposer qu'ils sont tous identiques. Ce n'est pas la forme de chaque grain qui va nous intéresser, mais la façon dont un immense nombre de grains interagissent pour finalement former des dunes.
Maintenant, rapprochons nous. Posons nous sur la pente d'une dune, et rapprochons nous encore. Jusqu'à distinguer les différents grains, le nez tout contre le sol. On se rend alors compte que les grains sont empilés de façon à constituer une pente. En d'autres termes, on peut voir, en simplifiant, la dune comme des colonnes de grains empilés les uns sur les autres. Bien sûr, un grain peut être à cheval entre deux colonnes, mais nous supposerons pour simplifier que çe n'est pas le cas. Pour simplifier encore (c'est une activité bien importante lorsque la science tente de modéliser la réalité), nous allons seulement regarder le profil de la pente, c'est à dire une coupe de la dune à cet endroit-là.
Donc, pour résumer, nous nous intéressons ici à des profils de pentes de dunes, constituées de piles de grains. Le profil peut être vu comme une suite de colonnes de grains, celles-ci étant de moins en moins hautes de gauche à droite, comme représenté sur la figure 1. Soulignons que, comme nous l'avons déjà signalé, nous ne considérons pas des profils qui montent et qui descendent mais seulement des profils qui descendent (de gauche à droite).
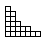
Figure 1. Un exemple de profil de dune abstrait : une suite de colonnes de grains, de hauteurs décroissantes de gauche à droite. Comme la forme des grains n'a pas d'importance dans ce qui nous intéresse ici, nous les représentons par des carrés.
Nous allons étudier dans cet article l'ensemble de tous les profils de dunes possibles. En d'autres termes, quelles sont toutes les formes qu'on peut obtenir et qui correspondent effectivement à des profils de dunes tels que nous les avons définis ? En particulier, comment obtenir toutes ces formes ? C'est cette dernière question qui va retenir toute notre attention, et nous donner l'occasion de réfléchir un peu ensemble.
Ces réflexions vont nous donner l'occasion de nous pencher sur la notion de démonstration mathématiques. Nous allons même en faire ensemble ! Ce seront des parties un peu plus difficiles à suivre, mais ça vaut le coup : c'est une bonne occasion de savoir comment sont établie les vérités scientifiques. Et les démonstrations que nous allons faire ensemble restent relativement simples. Vous pouvez toutefois les sauter en première lecture, c'est pourquoi elles sont mises à part dans le texte. Mais essayez de les comprendre, éventuellement en vous aidant de petits dessins. C'est là qu'est la réflexion...
Commençons doucement. Avec un seul grain, il y a un seul profil de dune possible. Avec deux grains, il y a deux profils possibles, et avec trois grains il y a trois possibilités, comme montré figure 2. Avec quatre grains, les choses se compliquent un peu : on obtient cinq profils possibles, comme montré figure 3.

Figure 2. À gauche, les deux profils possibles avec deux grains. Puis, les trois profils possibles avec trois grains. À droite, une construction possible avec trois grains que nous ne considérons pas comme une profil car les colonnes ne sont pas de hauteurs décroissantes de gauche à droite.

Figure 3. Les cinq profils possibles avec quatre grains.
On aimerait pouvoir construire les profils possibles en étant sûr de ne pas en oublier. Quand on n'a que quelques grains, comme dans les exemples que nous venons de développer, ça n'est pas difficile. Mais comment faire quand le nombre de grains grandit ? Ceci est d'autant plus délicat que le nombre de profils possibles grandit très vite : avec dix grains, il y a 42 profils possibles, avec vingt, 627 profils, et avec trente, 5604. Le nombre de possibilités ne cesse de croître, et à une vitesse effrénée.
Il nous faut donc une méthode rigoureuse pour pouvoir donner tous les profils possibles avec un nombre donné n de grains.
Une première idée.
Une première solution est de construire ces profils à partir de ceux contenant n-1 grains. Puisqu'on sait construire les profils possibles avec quatre grains (figure 3), on pourra alors construire ceux avec cinq grains, donc ensuite ceux avec six grains, et ainsi de suite jusqu'au n donné.
Dessinons sur une ligne le seul profil possible avec un grain. Puis, sur la ligne au-dessous, dessinons les profils possibles obtenus à partir de celui-là en ajoutant un grain. Et continuons ainsi : sur chaque ligne, on dessine les profils obtenus en ajoutant un grain sur une colonne d'un profil de la ligne du dessus. Puis, comme montré sur la figure 4, relions deux profils si l'un est obtenu à partir de l'autre en ajoutant un grain. On obtient un diagramme dans lequel chaque ligne ne contient que des profils contenant le même nombre de grains. Plus précisément, la n-ième ligne contient des profils avec n grains. Voir figure 4.
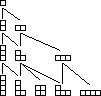
Figure 4. Les quatre premières lignes du diagramme dont chaque ligne est obtenue à partir de la précédente en ajoutant un grain sur les colonnes des profils qui y figurent.
Mais est-il bien clair qu'on obtient de cette façon tous les profils possibles ? Comment s'en assurer ? C'est exactement à ça que servent les démonstrations.
|
Démonstration. Supposons que notre méthode ne marche pas. Ceci signifie que, quelque part dans le diagramme, il manque un profil possible. Prenons la première ligne sur laquelle un profil manque, et disons que c'est la n-ième. Ceci signifie plusieurs choses. En premier lieu, n est plus grand que 1 car la première ligne, qui contient un seul élément, est évidemment complète. De plus, la ligne précédant la n-ième ligne contient bien tous les profils possibles avec n-1 grains, puisque n est le numéro de la première ligne incomplète. Considérons maintenant un profil manquant qui devrait être sur la ligne n. Considérons la dernière colonne, celle la plus à droite de ce profil, qui contienne au moins un grain. Si on enlève un grain à cette colonne, qu'obtient-on ? On a forcément un profil contenant n-1 grains, et ce profil est valide : avoir diminué la hauteur de la dernière colonne d'une unité ne peut pas avoir conduit à autre chose qu'une suite de colonnes décroissantes. Par conséquent, le profil que nous avons obtenu est dans la ligne n-1, puisque celle-ci est complète. Mais à partir de ce profil, on peut obtenir le profil dont nous étions partis (il suffit de rajouter un grain sur la dernière colonne), et donc il est dans la n-ième ligne, puisque c'est comme ça qu'on l'a construite. Mais justement, nous avions choisi un profil qui n'était pas dans le diagramme (rappelez-vous le début) ! Donc il y a une contradiction. Si nous obtenons une contradiction au bout d'un raisonnement logique comme celui que nous venons de faire, ça signifie tout simplement que l'hypothèse de départ était fausse. Or, quelle était notre hypothèse ? Justement que notre méthode ne marchait pas ! Cette hypothèse est fausse ? Ceci signifie exactement que notre méthode marche. Nous l'avons démontré en utlisant une technique classique appleée démonstration par l'absurde : on suppose le contraire de ce qu'on veut démontrer, puis on arrive à une contradiction, donc l'hypothèse est fausse, donc son contraire, qui est exactement ce que nous voulions démontrer, est vrai. |
Comment utiliser le diagramme lorsque nous voulons dessiner tous les profils possibles avec un certain nombre n de grains ? Il s'agit en fait de dessiner la n-ième ligne. Pour ce faire, on dessine toutes les lignes qui la précèdent, de la façon suivante. Si on a déjà construit une certaine ligne, disons la numéro i, on construit la suivante en prenant chaque profil de la ligne i puis en cherchant toutes les colonnes sur lesquelles on peut ajouter un grain. C'est facile, ce sont tout simplement les colonnes qui sont plus petites que leur voisine de gauche (et en plus la colonne la plus à gauche ainsi que la première colonne vide à droite). On obtient ainsi un certain nombre de profils. Pour chacun d'eux, s'il n'a pas déjà été dessiné sur la ligne suivante, on le dessine. De plus, on le relie au profil à partir duquel on vient de l'obtenir. Essayez de construire de cette façon la cinquième ligne du diagramme à partir de la figure 4 (la solution est donnée figure 5).
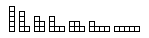
Figure 5. La cinquième ligne du diagramme, c'est-à-dire tous les profils contenant cinq grains.
Une meilleure solution.
Nous venons de trouver une solution à notre problème, c'est-à-dire une méthode pour trouver tous les profils possibles avec n grains. Toutefois, cette méthode a un gros inconvénient : on doit trouver tous les profils possibles pour tous les nombres de grains inférieurs à n. Au final, on a donc dessiné beaucoup plus de profils que ceux que nous voulions obtenir. Serait-il possible de trouver une méthode qui donne exactement tous les profils possibles avec n grains, et rien d'autre ?
Un principe susceptible de nous amener à une telle méthode est de trouver une règle transformant un profil en un autre. Il faudrait que cette règle nous permette, en l'appliquant autant de fois que possible à partir d'un profil, d'obtenir tous les autres profils possibles avec n grains.
Remarquons tout d'abord que la règle que nous recherchons doit être une règle de déplacement des grains, puisque le nombre de grains avant et après l'application de la règle est le même, n. De plus, nous recherchons une règle simple, puisque nous allons vouloir, pour notre plus grand plaisir, démontrer ses propriétés. Nous cherchons donc une règle qui déplace un seul grain à la fois. Enfin, nous devons choisir un profil de départ qui soit lui aussi très simple, et existe pour toutes les valeurs possibles de n.
Prenons par exemple comme profil initial celui composé d'une
seule colonne de n grains. C'est bien un profil valide.
Puis, rappelons-nous que nous sommes en train d'étudier
des tas de sable, et introduisons donc la règle suivante :
un grain peut tomber d'un colonne à sa voisine de droite si
le profil obtenu est toujours valide (c'est-à-dire si les
colonnes ont toujours des hauteurs décroissantes de gauche
à droite après la chute). Par exemple, pour n=7,
on commence avec  . Puis on obtient
d'abord
. Puis on obtient
d'abord  . On peut continuer :
à l'étape d'après, on obtient
. On peut continuer :
à l'étape d'après, on obtient 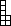 .
À ce moment là, quelque chose se passe :
on a deux choix. On peut faire tomber un grain de la
première colonne vers la seconde, ou de la seconde vers la
troisième. Dans le premier choix, on obtient
.
À ce moment là, quelque chose se passe :
on a deux choix. On peut faire tomber un grain de la
première colonne vers la seconde, ou de la seconde vers la
troisième. Dans le premier choix, on obtient  ,
et dans le second on obtient
,
et dans le second on obtient  .
On garde ces deux profils
et on continue. À partir de chacun d'eux,
on n'a qu'une possibilité pour faire tomber un grain.
À partir de la première on obtient
.
On garde ces deux profils
et on continue. À partir de chacun d'eux,
on n'a qu'une possibilité pour faire tomber un grain.
À partir de la première on obtient 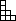 ,
et à partir de la seconde, on obtient...
,
et à partir de la seconde, on obtient... 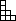 également ! Donc, on avait un profil à
partir duquel on pouvait obtenir deux profils différents,
qui à leur tour donnent un seul et même profil.
On continue à partir de ce profil, et on
obtient successivement
également ! Donc, on avait un profil à
partir duquel on pouvait obtenir deux profils différents,
qui à leur tour donnent un seul et même profil.
On continue à partir de ce profil, et on
obtient successivement
 ,
,  et enfin
et enfin  ,
où plus rien n'est possible. Tout cela est résumé
dans la figure 6.
,
où plus rien n'est possible. Tout cela est résumé
dans la figure 6.
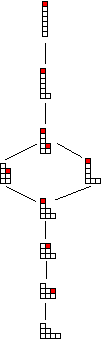
Figure 6. L'effondrement progressif d'une colonne de n=7 grains. Dans chaque profil, les grains pouvant tomber sont coloriés.
Tous les profils obtenus sont bien des profils contenant n=7
grains. Toutefois, il en manque. Par exemple, le profil composé
de 7 colonnes d'un seul grain n'est pas obtenu, alors que c'est
bien un profil valide. Et ce n'est pas le seul :
 manque aussi, ainsi que d'autres. Alors comment
modifier notre idée pour obtenir aussi ces possibilités ?
Une piste consiste déjà à se dire que, puisque notre
règle marche plutôt bien, on va la garder et lui ajouter une
possibilité. Mais laquelle ?... Avez-vous une
idée ?
manque aussi, ainsi que d'autres. Alors comment
modifier notre idée pour obtenir aussi ces possibilités ?
Une piste consiste déjà à se dire que, puisque notre
règle marche plutôt bien, on va la garder et lui ajouter une
possibilité. Mais laquelle ?... Avez-vous une
idée ?
Il y a plusieurs solutions. On peut par exemple autoriser un grain à glisser le long d'un plateau, c'est-à-dire que si on a une suite de colonnes toutes de même hauteur, précédée d'une colonne contenant un grain de plus et suivie d'une colonne en contenant un de moins, alors on peut faire glisser un grain de la colonne en contenant un de plus à celle en contenant un de moins. Ainsi, on obtient le diagramme de la figure 7, qui n'est rien d'autre que la version complètée de celui de la figure 6. On obtient cette fois tous les profils possibles. Et c'est toujours le cas, pour n'importe quelle valeur de n. Sauriez-vous le démontrer ?...
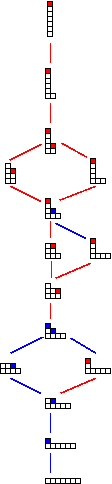
Figure 7. L'effondrement progressif d'une colonne de n=7 grains avec chutes et glissements de grains. Dans chaque profil, les grains pouvant bouger sont coloriés (en rouge pour les grains pouvant tomber, en bleu pour les grains pouvant glisser). De plus, les traits correspondant à une chute sont rouges, ceux correspondant à un glissement sont bleus.
|
Démonstration. Considérons un profil possible avec n grains, n'importe lequel. Nous allons faire remonter vers la gauche les grains des colonnes de droite en faisant des chutes et des glissements à l'envers. Autrement dit, à partir de n'importe quel profil, nous allons montrer qu'on peut prendre un grain à droite et le déplacer vers la gauche. En répétant l'opération, on obtiendra donc une colonne de n grains, à partir de laquelle, en refaisant le chemin à l'envers (donc en remettant les chutes et les glissements dans le bon sens), on peut obtenir le profil dont nous étions partis. N'importe quel profil sera donc obtenu avec des chutes et des glissements de grains à partir de la colonne de n grains, ce qui montre bien que notre méthode donne tous les profils possibles.
Voyons comment ça se passe sur un exemple. Considérons le profil
Tout d'abord, on ne peut faire remonter un grain qu'à partir d'une colonne qui est strictement plus haute que la suivante, sinon un crée un trou. Nous supposons donc que nous sommes dans ce cas. Maintenant, quand peut-on faire une chute à l'envers ? Quand la colonne de laquelle on veut faire remonter un grain est précédée de deux colonnes qui ne font pas la même hauteur. Et quand peut-on faire un glissement à l'envers ? Exactement quand la colonne de laquelle on veut faire remonter un grain est de la même hauteur que la précédente et celle d'avant (et éventuellement d'autres encore avant elles). Si ces remarques ne sont pas claires pour vous, prenez un instant pour faire quelques croquis afin de vous convaincre de leur véracité ; c'est le point délicat de cette démonstration, et c'est important pour la suite. Donc, on peut faire remonter un grain d'une colonne si celle-ci est plus haute que la suivante, et que celle qui précède est plus petite que celle encore avant (chute à l'envers), ou si elles sont toutes trois de même hauteur (glissement à l'envers). On peut donc toujours faire remonter le grain du sommet de la dernière colonne, sauf si celle-ci est plus petite que la précédente, et que cette dernière est de même hauteur que celle encore avant. C'est dans ce cas qu'on est bloqué. Mais alors une remarque nous sauve : on peut faire remonter le grain de l'avant dernière colonne. En effet, celle-ci est de même hauteur que celle juste à sa gauche, et donc on peut faire un glissement à l'envers. En conclusion, on peut toujours faire remonter un grain de la dernière colonne ou de l'avant-dernière. Par conséquent, en répétant ces remontées autant de fois que nécessaire, on obtient un profil qui n'a plus que deux colonnes (sinon on peut continuer à faire remonter des grains de la dernière colonne ou de l'avant-dernière). Enfin, lorsqu'on n'a plus que deux colonnes, vous pouvez vérifier facilement que tous les grains de la seconde colonne peuvent être remontés un à un sur la première colonne, avec des chutes à l'envers. Finalement, on peut remonter les grains en faisant des chutes et des glissements à l'envers jusqu'à obtenir la colonne de n grains. Donc, à partir de la colonne de n grains, on peut, en effectuant les mêmes chutes et glissements mais dans le bon sens, obtenir le profil que nous avions considéré. Comme ceci est possible avec n'importe quel profil contenant n grains, on obtient le résultat souhaîté : on peut obtenir tous les profils contenant n grains à partir de la colonne de n grains en effectuant des chutes ou des glissements de grains. |
Pour conclure...
Nous avons étudié ensemble un modèle très simplifié de profils de dunes de sable. Nous nous sommes en particulier concentrés sur la façon d'obtenir toutes les pentes possibles avec un nombre donné de grains. Nous avons trouvé deux solutions à ce problème, et, plus important, nous avons démontré que ces deux méthodes marchent bien. Ceci n'est pas anodin, et mérite d'être souligné : nous n'avons pas seulement décrit des solutions qui semblent correctes intuitivement ; nous avons donné des preuves, des démonstrations mathématiques rigoureuses, du fait qu'elles résolvent bien le problème posé. Cette démarche est très générale et constitue une partie importante de l'activité scientifique : lorsqu'un scientifique est confronté à un problème, il le traduit d'abord en langage mathématique (c'est ce qu'on appelle la modélisation), puis il utilise son intuition pour trouver des solutions, qui ne sont considérées comme valides (par lui-même et par les autres scientifiques) que lorsqu'il a donné une démonstration rigoureuse de leurs propriétés. Vous l'avez compris, les dunes nous ont servi de prétexte pour vous offrir un exemple de cette démarche intellectuelle, dont nous espérons vous avoir donné un aperçu convainquant.